Another simple 3D pie chart with gnuplot (script included)

A couple of days ago, I showed how one can draw a very simple 2D pie chart embedded in 3D space in gnuplot. Today we will try our hand at a real 3D pie chart, especially, that we have basically learnt everything that we need in that post. The only extra step required is to draw the side of the cylinder, with the proper colouring. Once we do this, we get a figure similar to this one:

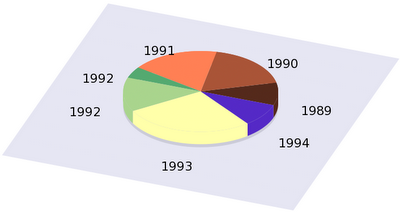
Using the data from the previous post, the gnu file would read as follows

reset                                                                     
b=0.4; a=0.4; B=0.5; r=1.0; s=0.1                                         
set view 30, 20; set parametric                                           
unset border; unset tics; unset key; unset colorbox                       
set ticslevel 0                                                           
set urange [0:1]; set vrange [0:1]                                        
set xrange [-2:2]; set yrange [-2:2]; set zrange [0:3]                    
set multiplot                                                             
set palette model RGB functions 0.9, 0.9,0.95                             
splot -2+4*u, -2+4*v, 0 w pm3d                                            
set palette model RGB functions 0.8, 0.8, 0.85                            
splot cos(u*2*pi)*v, sin(u*2*pi)*v, 0 w pm3d                              
set palette model RGB functions 0.333333, 0.166667, 0.111111              
set urange [0.000000:0.090909]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+v*a w pm3d                          
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+v*a w pm3d                      
set palette model RGB functions 0.666667, 0.333333, 0.222222              
set urange [0.090909:0.272727]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+v*a w pm3d                          
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+v*a w pm3d                      
set palette model RGB functions 1.000000, 0.500000, 0.333333              
set urange [0.272727:0.454545]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+v*a w pm3d                          
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+v*a w pm3d                      
set palette model RGB functions 0.333333, 0.666667, 0.444444              
set urange [0.454545:0.500000]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+v*a w pm3d                          
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+v*a w pm3d                      
set palette model RGB functions 0.666667, 0.833333, 0.555556              
set urange [0.500000:0.636364]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+v*a w pm3d                          
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+v*a w pm3d                      
set palette model RGB functions 1.000000, 1.000000, 0.666667              
set urange [0.636364:0.909091]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+v*a w pm3d                          
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+v*a w pm3d                      
set palette model RGB functions 0.333333, 0.166667, 0.777778              
set urange [0.909091:1.000000]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+v*a w pm3d                          
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+v*a w pm3d                      
set palette model RGB functions 0.333333, 0.166667, 0.111111              
set urange [0.000000:0.090909]                                            
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d                        
set palette model RGB functions 0.666667, 0.333333, 0.222222              
set urange [0.090909:0.272727]                                            
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d                        
set palette model RGB functions 1.000000, 0.500000, 0.333333              
set urange [0.272727:0.454545]                                            
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d                        
set palette model RGB functions 0.333333, 0.666667, 0.444444              
set urange [0.454545:0.500000]
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d
set palette model RGB functions 0.666667, 0.833333, 0.555556
set urange [0.500000:0.636364]
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d
set palette model RGB functions 1.000000, 1.000000, 0.666667
set urange [0.636364:0.909091]
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d
set label 1 "1989" at cos(0.090909*pi)*B+cos(0.090909*pi), sin(0.090909*pi)*B+sin(0.090909*pi) centre
set label 2 "1990" at cos(0.363636*pi)*B+cos(0.363636*pi), sin(0.363636*pi)*B+sin(0.363636*pi) centre
set label 3 "1991" at cos(0.727273*pi)*B+cos(0.727273*pi), sin(0.727273*pi)*B+sin(0.727273*pi) centre
set label 4 "1992" at cos(0.954545*pi)*B+cos(0.954545*pi), sin(0.954545*pi)*B+sin(0.954545*pi) centre
set label 5 "1992" at cos(1.136364*pi)*B+cos(1.136364*pi), sin(1.136364*pi)*B+sin(1.136364*pi) centre
set label 6 "1993" at cos(1.545455*pi)*B+cos(1.545455*pi), sin(1.545455*pi)*B+sin(1.545455*pi) centre
set label 7 "1994" at cos(1.909091*pi)*B+cos(1.909091*pi), sin(1.909091*pi)*B+sin(1.909091*pi) centre
set palette model RGB functions 0.333333, 0.166667, 0.777778
set urange [0.909091:1]
splot cos(u*2*pi)*v, sin(u*2*pi)*v, a+s w pm3d
unset multiplot

However, since you don't want to insert all these numbers by hand, I attach a small script in gawk, that would produce the gnu file for you by the stroke of a key. Here you go:

#!/bin/bash

gawk  'BEGIN {i=0}
{
if($0!~/#/) {
 label[i] = $1
 v[i] = $2
 D+= $2
 i++
}
}
END {
print "reset"
print "b=0.4; a=0.4; B=0.5; r=1.0; s=0.1"
print "set view 30, 20; set parametric"
print "unset border; unset tics; unset key; unset colorbox"
print "set ticslevel 0"
print "set urange [0:1]; set vrange [0:1]"
print "set xrange [-2:2]; set yrange [-2:2]; set zrange [0:3]"
print "set multiplot"
print "set palette model RGB functions 0.9, 0.9,0.95"
print "splot -2+4*u, -2+4*v, 0 w pm3d"
print "set palette model RGB functions 0.8, 0.8, 0.85"
print "splot cos(u*2*pi)*v, sin(u*2*pi)*v, 0 w pm3d"
d=0.0;
for(j=0;j<i;j++) {
 printf "set palette model RGB functions %f, %f, %f\n", (j%3+1)/3, (j%6+1)/6, (j%9+1)/9
 printf "set urange [%f:%f]\n", d, d+v[j]/D
 print "splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+v*a w pm3d"
 print "splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+v*a w pm3d"
 d+=v[j]/D
}

d=0.0;
for(j=0;j<i-1;j++) {
 printf "set palette model RGB functions %f, %f, %f\n", (j%3+1)/3, (j%6+1)/6, (j%9+1)/9
 printf "set urange [%f:%f]\n", d, d+v[j]/D
 print "splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d"
 d+=v[j]/D
}
d=v[0]/D;
for(j=0;j<i;j++) {
 printf "set label %d \"%s\" at cos(%f*pi)*B+cos(%f*pi), sin(%f*pi)*B+sin(%f*pi) centre\n", j+1, label[j], d, d, d, d
 d=d+v[j]/D+v[j+1]/D
}
printf "set palette model RGB functions %f, %f, %f\n", ((i-1)%3+1)/3, ((i-1)%6+1)/6, ((i-1)%9+1)/9
printf "set urange [%f:1]\n", 1.0-v[i-1]/D
print "splot cos(u*2*pi)*v, sin(u*2*pi)*v, a+s w pm3d"
print "unset multiplot"

}' $1

You don't even need to write the gnu file to disc, you can call the gawk script from gnuplot as

load "<pie3d.sh pie.dat

Now, this is not everything. I have recently seen pie charts that are not full, i.e., the centre is missing, as in this one

It is very easy to hack our gnu file above to achieve something like this: the only thing we have to do is to restrict the dummy variable in the parametric plot, so that instead of 0 to 1, now it runs from 0.5 to 1. However, when doing this, we have got to be a bit careful: that particular dummy variable appears at more than one place, so we have to make sure that the actual range doesn't change where we don't want it to change. The snag is that these ranges are linked to each other. But that shouldn't be a problem! In the script below, I highlighted the places to which we have got to pay particular attention.

reset                                                                     
b=0.4; a=0.4; B=0.5; r=1.0; s=0.1                                         
set view 30, 20; set parametric                                           
unset border; unset tics; unset key; unset colorbox                       
set ticslevel 0                                                           
set urange [0:1]; set vrange [0.5:1]                                      
set xrange [-2:2]; set yrange [-2:2]; set zrange [0:3]                    
set multiplot                                                             
set palette model RGB functions 0.9, 0.9,0.95                             
splot -2+4*u, -2+4*(1-v)*2, 0 w pm3d                                      
set palette model RGB functions 0.8, 0.8, 0.85                            
splot cos(u*2*pi)*v, sin(u*2*pi)*v, 0 w pm3d                              
set palette model RGB functions 0.333333, 0.166667, 0.111111              
set urange [0.000000:0.090909]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+(1-v)*a*2 w pm3d                    
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+(1-v)*a*2 w pm3d                
set palette model RGB functions 0.666667, 0.333333, 0.222222              
set urange [0.090909:0.272727]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+(1-v)*a*2 w pm3d                    
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+(1-v)*a*2 w pm3d                
set palette model RGB functions 1.000000, 0.500000, 0.333333              
set urange [0.272727:0.454545]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+(1-v)*a*2 w pm3d                    
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+(1-v)*a*2 w pm3d                
set palette model RGB functions 0.333333, 0.666667, 0.444444              
set urange [0.454545:0.500000]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+(1-v)*a*2 w pm3d                    
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+(1-v)*a*2 w pm3d                
set palette model RGB functions 0.666667, 0.833333, 0.555556              
set urange [0.500000:0.636364]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+(1-v)*a*2 w pm3d                    
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+(1-v)*a*2 w pm3d                
set palette model RGB functions 1.000000, 1.000000, 0.666667              
set urange [0.636364:0.909091]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+(1-v)*a*2 w pm3d                    
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+(1-v)*a*2 w pm3d                
set palette model RGB functions 0.333333, 0.166667, 0.777778              
set urange [0.909091:1.000000]                                            
splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+(1-v)*a*2 w pm3d                    
splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+(1-v)*a*2 w pm3d                
set palette model RGB functions 0.333333, 0.166667, 0.111111              
set urange [0.000000:0.090909]                                            
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d                        
set palette model RGB functions 0.666667, 0.333333, 0.222222              
set urange [0.090909:0.272727]                                            
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d                        
set palette model RGB functions 1.000000, 0.500000, 0.333333              
set urange [0.272727:0.454545]                                            
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d                        
set palette model RGB functions 0.333333, 0.666667, 0.444444              
set urange [0.454545:0.500000]
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d
set palette model RGB functions 0.666667, 0.833333, 0.555556
set urange [0.500000:0.636364]
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d
set palette model RGB functions 1.000000, 1.000000, 0.666667
set urange [0.636364:0.909091]
splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d
set label 1 "1989" at cos(0.090909*pi)*B+cos(0.090909*pi), sin(0.090909*pi)*B+sin(0.090909*pi) centre
set label 2 "1990" at cos(0.363636*pi)*B+cos(0.363636*pi), sin(0.363636*pi)*B+sin(0.363636*pi) centre
set label 3 "1991" at cos(0.727273*pi)*B+cos(0.727273*pi), sin(0.727273*pi)*B+sin(0.727273*pi) centre
set label 4 "1992" at cos(0.954545*pi)*B+cos(0.954545*pi), sin(0.954545*pi)*B+sin(0.954545*pi) centre
set label 5 "1992" at cos(1.136364*pi)*B+cos(1.136364*pi), sin(1.136364*pi)*B+sin(1.136364*pi) centre
set label 6 "1993" at cos(1.545455*pi)*B+cos(1.545455*pi), sin(1.545455*pi)*B+sin(1.545455*pi) centre
set label 7 "1994" at cos(1.909091*pi)*B+cos(1.909091*pi), sin(1.909091*pi)*B+sin(1.909091*pi) centre
set palette model RGB functions 0.333333, 0.166667, 0.777778
set urange [0.909091:1]
splot cos(u*2*pi)*v, sin(u*2*pi)*v, a+s w pm3d
unset multiplot

Again, it is much easier to do this in a convenient way, so I give my gawk script below.

#!/bin/bash

gawk  'BEGIN {i=0}
{
if($0!~/#/) {
 label[i] = $1
 v[i] = $2
 D+= $2
 i++
}
}
END {
print "reset"
print "b=0.4; a=0.4; B=0.5; r=1.0; s=0.1"
print "set view 30, 20; set parametric"
print "unset border; unset tics; unset key; unset colorbox"
print "set ticslevel 0"
print "set urange [0:1]; set vrange [0.5:1]"
print "set xrange [-2:2]; set yrange [-2:2]; set zrange [0:3]"
print "set multiplot"
print "set palette model RGB functions 0.9, 0.9,0.95"
print "splot -2+4*u, -2+4*(1-v)*2, 0 w pm3d"
print "set palette model RGB functions 0.8, 0.8, 0.85"
print "splot cos(u*2*pi)*v, sin(u*2*pi)*v, 0 w pm3d"
d=0.0;
for(j=0;j<i;j++) {
 printf "set palette model RGB functions %f, %f, %f\n", (j%3+1)/3, (j%6+1)/6, (j%9+1)/9
 printf "set urange [%f:%f]\n", d, d+v[j]/D
 print "splot cos(u*2*pi)*r, sin(u*2*pi)*r, s+(1-v)*a*2 w pm3d"
 print "splot cos(u*2*pi)*r/2, sin(u*2*pi)*r/2, s+(1-v)*a*2 w pm3d"
 d+=v[j]/D
}

d=0.0;
for(j=0;j<i-1;j++) {
 printf "set palette model RGB functions %f, %f, %f\n", (j%3+1)/3, (j%6+1)/6, (j%9+1)/9
 printf "set urange [%f:%f]\n", d, d+v[j]/D
 print "splot cos(u*2*pi)*r*v, sin(u*2*pi)*r*v, s+a w pm3d"
 d+=v[j]/D
}
d=v[0]/D;
for(j=0;j<i;j++) {
 printf "set label %d \"%s\" at cos(%f*pi)*B+cos(%f*pi), sin(%f*pi)*B+sin(%f*pi) centre\n", j+1, label[j], d, d, d, d
 d=d+v[j]/D+v[j+1]/D
}
printf "set palette model RGB functions %f, %f, %f\n", ((i-1)%3+1)/3, ((i-1)%6+1)/6, ((i-1)%9+1)/9
printf "set urange [%f:1]\n", 1.0-v[i-1]/D
print "splot cos(u*2*pi)*v, sin(u*2*pi)*v, a+s w pm3d"
print "unset multiplot"

}' $1

Well, this is for today. So long!

Simple pie chart with Gnuplot

Addendum: I have noticed (just by looking at the backtracks of people who come to my blog) that for some reason, google won't tell you that there are recent developments on the pie chart. So, if you are interested, you should look at my post on the 1st Aug, 2009 (where I show how to make the pie chart entirely in gnuplot, without any external scripts), and also 31st May, 2009 (which is the 3D version of the present post.) 19 Aug 2009


Addendum 2: Hellson has provided a php variant of the script discussed below. (Thanks a lot for it!) If, for whatever reason, php suits your needs better, than gawk, you should check out his site 21 Aug 2009

Unfortunately, gnuplot hasn't got a built-in function for producing pie charts. This is a type of figure which is not extremely informative, but is quite popular. (At least, this is what I gather from people's asking for it all over the web.) Today, we will try our hands at making one in gnuplot. In gnuplot 4.3, there is a function with which arcs of circles can be drawn. However, this works only on 2D plots, so if you want to have something that looks like a 3D graph, you have got to work a bit harder. Here is the code that I used to generate the figure below.

reset

a1=0.1
a2=0.2
a3=0.15
a4=0.15
a5=0.3
a6=0.1

b=0.4
s=0.2
B=0.5

set view 30, 20
set parametric
unset border
unset tics
unset key
set ticslevel 0
unset colorbox
set urange [0:1]
set vrange [0:1]
set xrange [-2:2]
set yrange [-2:2]
set zrange [0:3]
set multiplot

# First, we draw the 'box' around the plotting volume
set palette model RGB functions 0.9, 0.9,0.95
splot -2+4*u, -2+4*v, 0 w pm3d

set palette model RGB functions 0.8, 0.8, 0.85

set urange [a1:1]
splot cos(u*2*pi)*v, sin(u*2*pi)*v, 0 w pm3d

set urange [0:a1]
splot cos(a1*pi)*b+cos(u*2*pi)*v, sin(a1*pi)*b+sin(u*2*pi)*v, 0 w pm3d

set palette model RGB functions 1, 0, 0
set urange [0:a1]
splot cos(a1*pi)*b+cos(u*2*pi)*v, sin(a1*pi)*b+sin(u*2*pi)*v, s w pm3d

set palette model RGB functions 0, 0.5, 0
set urange [a1:a1+a2]
splot cos(u*2*pi)*v, sin(u*2*pi)*v, s w pm3d

set palette model RGB functions 0, 0, 0.8
set urange [a1+a2:a1+a2+a3]
splot cos(u*2*pi)*v, sin(u*2*pi)*v, s w pm3d

set palette model RGB functions 0.8, 0, 0.8
set urange [a1+a2+a3:a1+a2+a3+a4]
splot cos(u*2*pi)*v, sin(u*2*pi)*v, s w pm3d

set palette model RGB functions 0.8, 0.8, 0
set urange [a1+a2+a3+a4:a1+a2+a3+a4+a5]
splot cos(u*2*pi)*v, sin(u*2*pi)*v, s w pm3d

set palette model RGB functions 0, 0.8, 0.8
set urange [a1+a2+a3+a4+a5:a1+a2+a3+a4+a5+a6]
set label 1 '1988' at  cos(a1*pi)*B+cos(a1*pi), sin(a1*pi)*B+sin(a1*pi)
D = 2*a1+a2
set label 2 '1989' at  cos(D*pi)*B+cos(D*pi), sin(D*pi)*B+sin(D*pi)
D=D+a2+a3
set label 3 '1990' at  cos(D*pi)*B+cos(D*pi), sin(D*pi)*B+sin(D*pi)
D=D+a3+a4
set label 4 '1991' at  cos(D*pi)*B+cos(D*pi), sin(D*pi)*B+sin(D*pi)
D=D+a4+a5
set label 5 '1992' at  cos(D*pi)*B+cos(D*pi), sin(D*pi)*B+sin(D*pi)
D=D+a5+a6
set label 6 '1993' at  cos(D*pi)*B+cos(D*pi), sin(D*pi)*B+sin(D*pi)
splot cos(u*2*pi)*v, sin(u*2*pi)*v, s w pm3d
unset multiplot

The values in the chart are defined in a1 through a6. (I made sure that they add up to one, so it is easier to work with them.) Then, we set up our figure in the usual way, and first we plot the plane and the shadow of the slices. In order to draw slices, we use a simple parametrisation of an arc of a circle, and shift the boundaries of the 'u' parameter. Note that one of the slices is off set, so it looks as if the pie chart had exploded. The extent to which the single slice is moved out is given by the value of 'b', while 'B' sets the distance of the labels from the centre.

Once we are done with this, we can set out to draw the actual slices. In order to colour them with a different colour, we change the palette as we proceed, and change the parameter range of 'u'. Before the last slice, we put out the labels as well, so that they will be displayed when the last piece is drawn.

Now, this seems to be a bit convoluted, and more importantly, it's quite inconvenient to put all values in by hand. So, what about a simple script to produce the gnu script? One possible implementation in gawk is given here.

#!/bin/bash
gawk  'BEGIN {i=0}
{
if($0!~/#/) {
label[i] = $1
v[i] = $2
D+= $2
i++
}
}
END {
print "reset"
print "b=0.4; a=0.2; B=0.5"
print "set view 30, 20; set parametric"
print "unset border; unset tics; unset key; unset colorbox"
print "set ticslevel 0"
print "set urange [0:1]; set vrange [0:1]"
print "set xrange [-2:2]; set yrange [-2:2]; set zrange [0:3]"
print "set multiplot"
print "set palette model RGB functions 0.9, 0.9,0.95"
print "splot -2+4*u, -2+4*v, 0 w pm3d"
print "set palette model RGB functions 0.8, 0.8, 0.85"
printf "set urange [%f:1]\n", v[0]/D
print "splot cos(u*2*pi)*v, sin(u*2*pi)*v, 0 w pm3d"
printf "set urange [0:%f]\n", v[0]/D
printf "splot cos(%f*pi)*b+cos(u*2*pi)*v, sin(%f*pi)*b+sin(u*2*pi)*v, 0 w pm3d\n", v[0]/D, v[0]/D
print "set palette model RGB functions 1, 0, 0"
printf "set urange [0:%f]\n", v[0]/D
printf "splot cos(%f*pi)*b+cos(u*2*pi)*v, sin(%f*pi)*b+sin(u*2*pi)*v, a w pm3d\n", v[0]/D, v[0]/D
d=v[0]/D
for(j=0;j<i-1;j++) {
printf "set palette model RGB functions %f, %f, %f\n", (j%3+1)/3, (j%6+1)/6, (j%9+1)/9
printf "set urange [%f:%f]\n", d, d+v[j]/D
print "splot cos(u*2*pi)*v, sin(u*2*pi)*v, a w pm3d"
d+=v[j]/D
}
d=v[0]/D
for(j=0;j<i-1;j++) {
printf "set label %d \"%s\" at cos(%f*pi)*B+cos(%f*pi), sin(%f*pi)*B+sin(%f*pi)\n", j+1, label[j], d, d, d, d
d=d+v[j]/D+v[j+1]/D
}
printf "set label %d \"%s\" at cos(%f*pi)*B+cos(%f*pi), sin(%f*pi)*B+sin(%f*pi)\n", i, label[i-1], d, d, d, d
printf "set palette model RGB functions %f, %f, %f\n", (i%3+1)/3, (i%6+1)/6, (i%9+1)/9
printf "set urange [%f:1]\n", 1.0-v[i-1]/D
print "splot cos(u*2*pi)*v, sin(u*2*pi)*v, a w pm3d"
print "unset multiplot"
}' $1

This is really nothing but the mechanical implementation of our gnuplot script. The only difference with respect to that is that we had to set the colour palette mechanically, which I did by giving the values (j%3+1)/3, (j%6+1)/6, (j%9+1)/9. If you are not satisfied with the colouring of your output, you can easily tamper with this, and get something that you like more.

Now, if you make this executable and call it, pie.sh, say, and have a file with two columns, the first one being the label for a particular value, then you can simple call this script from gnuplot as

gnuplot> load "< ./pie.sh pie.dat" 

Given the input file, pie.dat,

# This is a simple data file to test our script
# Note that the second column doesn't add up to 1.
# But this is not a problem, for the script normalises that:)
1989 0.1
1990 0.2
1991 0.2
1992 0.05
1992 0.15
1993 0.3
1994 0.1

I get this figure, which is quite OK, as far as the colouring is concerned.

3D bargraphs in gnuplot, once again

A couple of days ago, we discussed a quick and dirty (well, dirty, at least) way to generate 3D-looking bargraphs with gnuplot. There is another one (this time again with cylinders), which produces real-looking cylinders, like in this figure

The key to it is the 'phonging' procedure that we used yesterday to make that cute little sphere. So, here is the code. For ease of use, I defined the values that we want to plot in f1...f7 at the beginning of the file.

reset

A=-1
B=7
C=-4
D=3

# These are the actual values to be plotted
f1 = 1.0
f2 = 1.3
f3 = 0.4
f4 = 1.5
f5 = 1.9
f6 = 1.1
f7 = 0.9

# Radius of cylinders
r = 0.4
# Vertical position of 'phong' point
vp = 1.0

unset key
unset colorbox
set sample 100
set isosample 50, 50
set parametric
set urange [0:1]
set vrange [0:1]

set xrange [A:B]
set yrange [C:D]

# Basically, this is the definition of our cylinder

set table 'test.dat'
splot r*sin(2*pi*u), r*cos(2*pi*u), v,\
r*sin(2*pi*u)*v, r*cos(2*pi*u)*v, 1 w pm3d
unset table

set multiplot
set zrange [0:2]
unset xtics
unset ytics
set ztics out
set grid ztics
set ticslevel 0

# First, we draw the 'box' around the plotting volume
set palette model RGB functions 0.9, 0.9,0.95
splot A+(B-A)*u, C+(D-C)*v,0 w pm3d

# These are the vertical panes, with a gradient along
set palette model RGB functions 0.9, 0.9, 0.7+gray/5.0
splot A, C+(D-C)*u, 2*v w pm3d, A+(B-A)*u, D, 2*v w pm3d

set border 1+2+4+8+16+32+64+256+512
f(x,a,b) = 0.9*exp(-(x-a)*(x-a)/b/b)
set palette model RGB function gray, gray, 1
sp 'test.dat' u 1:2:($3*f1):(f($3*f1,vp,0.8)*f($1,0.3,0.2)*f($2,-0.3,0.2)) w pm
'' u ($1+1):2:($3*f2):(f($3*f2,vp,0.8)*f($1+1,1.3,0.2)*f($2,-0.3,0.2)) w pm3d,\
'' u ($1+2):2:($3*f3):(f($3*f3,vp,0.8)*f($1+2,2.3,0.2)*f($2,-0.3,0.2)) w pm3d,\
'' u ($1+3):2:($3*f4):(f($3*f4,vp,0.8)*f($1+3,3.3,0.2)*f($2,-0.3,0.2)) w pm3d,\
'' u ($1+4):2:($3*f5):(f($3*f5,vp,0.8)*f($1+4,4.3,0.2)*f($2,-0.3,0.2)) w pm3d,\
'' u ($1+5):2:($3*f6):(f($3*f6,vp,0.8)*f($1+5,5.3,0.2)*f($2,-0.3,0.2)) w pm3d,\
'' u ($1+6):2:($3*f7):(f($3*f7,vp,0.8)*f($1+6,6.3,0.2)*f($2,-0.3,0.2)) w pm3d

unset multiplot

If you look at it, this code is really nothing more than what we have already seen in previous days: apart from the general set-up commands, we plot the cylinder first to a file, (this time, we put on the cap, too), then draw the box in which we plot the bars. To make it more interesting, the vertical panes are given some gradient. You can check out the details of this in my previous post.

Finally, the cylinders are plotted one by one. Each time a new cylinder is processed, we shift it to the right, so that it doesn't overlap with the previous ones. To make the cylinders 3D-looking, we add the phong, as we discussed it yesterday. If you find that the white spot (actually, it is not completely white, but some very faint shade of blue, some steel-like colour) is too tight, you can ease up a bit on the Gaussian function. You can also shift the vertical position of the centre of the spot by tampering with the value of 'vp', somewhere at the beginning.


Again, it shouldn't be a problem to script the whole procedure. Once I have some time, I will do that and post it here. Till then!

Graphs on a background with gradient

Sometimes one would like to have a graph whose background is not so monotonic. This is especially useful in presentations. There is a relatively easy way to come up with a solution for this. Again, we will use multiplot, and plot the background on plots different to the main plot. First, here is the figure, that we have

and here is the code that produced it

reset
f(x) = exp(-x/10.0)*sin(x)
g(x) = exp(-x/10.0)
h(x) = -exp(-x/10.0)
set sample 30
set table 'test.dat'
plot [0:20] f(x)+(rand(0)-0.5)*0.2
unset table

set sample 100

set multiplot
set palette model RGB functions 0.4+gray/1.667, 0.75+gray/4.0, 0.4+gray/1.667
set pm3d map
set isosample 100,100
set yrange [-1:1]
unset colorbox
unset border
unset xtics
unset ytics
set size 1.5,1.6
set origin -.25,-.3
splot y t ''

set palette model RGB functions 0.9+gray/10.0, 0.5+gray/2.0, 0.5+gray/2.0
set size 1.208, 1.295
set origin -0.065,-0.125
splot [0:20] y  t ''

set size 1,1
set origin 0,0
set xtics
set ytics
set xlabel 'Time [s]'
set ylabel 'Position [m]'
set border 1+2+4+8
set key reverse box

plot [0:20] f(x) w l lt 3 lw 2 t 'y=sin(x)*exp(-x/10) ', \
g(x) w l lt rgb "#008800" t '', h(x) w l lt rgb "#008800" t '', \
'test.dat' u 1:2:($2-rand(0)*0.1-0.05):($2+rand(0)*0.1+0.05) w errorb pt 13 lt 1 t 'Data set 2 '

unset multiplot

Now, let us see what is happening here. The first couple of lines are there just to produce some data (in this case, a damped oscillation with some random noise). The interesting part begins with 'set multiplot': we define a palette, which will run between some shade of green and white. This will be our background for the whole image. It will have a gradient, because we plot the function 'y', so as we go towards the top, the colour becomes whiter and whiter. In order to cover the whole canvas, we have to play with the size a bit, but this should be more or less straightforward.


In the second plot, the only thing that really is different is the colour palette, which, this time, is from some shade of red to white. Again, you might have to set the size of the plot by hand, and this might also depend on the actual terminal that you are using.

In the last part, we set the labels and the border (if you cast a glance at the code, you'll notice that these were switched off at the beginning), and plot our functions and data. Since I wanted to show errorbars, I generated artificial errors with the rand(0) function. If you have a real data set that you want to plot, this should be much simpler. You can skip the first 7 lines, and just use the columns in your data file to show the errors.


There, you have it!

Phonged surfaces with Gnuplot

Another cool feature of a figure is its shininess, which is usually called phong, and gives the impression of three-dimensionality. I will show a relatively easy way to achieve this in Gnuplot. With a few lines of code, we can produce a figure that looks like this one:

The only thing that is required is to note that in 'pm3d', colouring can be given specified by an arbitrary function in the fashion

splot 'some.dat' using 1:2:3:(f(...)) with pm3d

where 'some.dat' contains our data, and f(...) denotes the function according to which we would like to colour the surface. The snag here is that this works only for data files where the surface is given as a x,y,z(x,y) triplet, but it won't do any good with functions. So, the first thing is to produce the surface data. This can easily be done by redirecting the plot to a table, which we will read back immediately. As in the figure above, I will plot a sphere, thus we write something like this:

set isosample 100,100
set parametric
set urange [0:1]
set vrange [0:1]
set table 'test.dat'
splot r*cos(2*pi*u)*sin(pi*v), r*sin(2*pi*u)*sin(pi*v), r*cos(pi*v)
unset table

This writes 10 000 points of a sphere to the file 'test.dat'. Having created the surface, we have got to plot it, and give it the phong. We assume for the time being that the surface is red, and where light impinges on it, it is shining white. Therefore, we need a palette that runs from red to white, and it doesn't contain other colours. (This is a bit of a bumpy statement, but you get the meaning.) The one below will do: it is red, when the palette function's argument is 0, and glowing white, when the palette function takes the argument of 1.

g(x) = x
b(x) = x
set palette model RGB functions 1, g(gray), b(gray)

Finally, we have to define the function itself. I am somewhat simple-minded, so I will just take a Gaussian function, and shift it in such a way that it takes the value 1, where I want to have the phong.

Having these in mind, the complete code for the figure above reads as

reset
unset key
unset colorbox
set pm3d scansbackward
set isosample 100,100
unset ztics
unset xtics
unset ytics
set border 1+2+4+8

r = 1.0
x0 = -0.2*r
z0 = 0.7*r
y0 = -r*sqrt(1.0-x0*x0)

set parametric
set urange [0:1]
set vrange [0:1]
set table 'test.dat'
splot r*cos(2*pi*u)*sin(pi*v), r*sin(2*pi*u)*sin(pi*v), r*cos(pi*v)

unset table

set multiplot
set ticslevel 0

set xrange [-4*r:4*r]
set yrange [-4*r:4*r]
set zrange [-r:3.2*r]

# First, we draw the plane on which the sphere rests
set palette model RGB functions 1, 254.0/255.0, 189.0/255.0
splot -4*r+8*r*u, -4*r+8*r*v, -1 w pm3d

# Then, the shadow of the sphere
# This shall be an ellipse
set palette model RGB functions 0.8, 0.8, 0.8
splot (1.5*r*cos(2*pi*u)*v+r/sqrt(2.0)), (r*sin(2*pi*u)*v+r/sqrt(2.0)), -1 w pm

# And finally, the sphere itself
g(x) = x
b(x) = x
f(x,a,b) = exp(-(x-a)*(x-a)/b/b)
set palette model RGB functions 1, g(gray), b(gray)
splot 'test.dat' u 1:2:3:(f($3,z0,0.4)*f($1,x0,0.4)*f($2,y0,0.4)) w pm3d
unset multiplot

Note that we applied our Gaussian function in the last but one line, to give the phong at z=0.7, (3rd column in the data file) x=-0.2, (1st column in the data file), and y=0.98 (2nd column in the data file). The phong positions were defined somewhere at the beginning, as z0, x0, and y0. Also note that by changing the 3rd argument in the function, the tightness of the white spot can be modified: smaller value will give smaller spot, and vice versa.

We need the multiplot only because we plotted a plane on which the sphere rests, and we also drew a gray ellipse, which is supposed to represent the shadow of the sphere. If you don't need shadows and the like, the code is much simpler, similar to this

reset
unset key
unset colorbox
set pm3d scansbackward
set isosample 150,150
unset ztics
unset xtics
unset ytics
set view 50, 30
set border 0
#set border 1+2+4+8

x0 = -1
z0 = 0.4
y0 = -2

set table 'test.dat'
splot [-6:6] [-6:6] sin(sqrt(x**2+y**2))/sqrt(x**2+y**2)
unset table

set ticslevel 0
g(x) = x/1.2
b(x) = x
f(x,a,b) = exp(-(x-a)*(x-a)/b/b)
set palette model RGB functions 1, g(gray), b(gray)
splot 'test.dat' u 1:2:3:(f($3,z0,1.0)*f($1,x0,3.0)*f($2,y0,3.0)) w pm3d

which produces the wavy function:

Shaded 3D bargraphs in Gnuplot

So, you have been told that it is impossible to produce a three-dimensional bargraph in gnuplot. Well, this is not exactly true. While their value might be limited, they still look cool in a presentation or a poster. I will outline a way to produce 3D bargraphs with shade. For a start, we will plot cylinders, and then sometime later cubes and the like. Just to wet your appetite, I give the figure first, and then dissect the code that produced it.

And now, let us see the code. We will assume that we want to plot the following set of data

1987 1
1988 2
1989 1.5
1990 1.8
1991 1.1

Now, here is the full code

reset
set border 0
unset key
unset colorbox
set cbrange [-0.1:2]
set isosample 10,10
set sample 100
set parametric
set ticslevel 0

a=2
b=0.5
c=-0.5
d=5.5
e=(c+d)/2.0
f=(d-c)
r=0.2

set multiplot
set urange [0:1]
set vrange [0:1]
set yrange [c:d]
set xrange [c:d]
set zrange [0:2.5]
unset xtics
unset ytics
set ztics out
set grid ztics

# First, we draw the 'box' around the plotting volume
set palette model RGB functions 0.8, 0.8,0.8
splot 10*u-0.5, c+f*v,0 w pm3d

set palette model RGB functions 1, 254.0/255.0, 189.0/255.0
splot -0.5, c+f*u, 2.5*v w pm3d , 10*u-0.5, d, 2.5*v w pm3d

set border 1+2+4+8+16+32+64+256+512
# Then we put on all the shadow. This step can be skipped
set palette model RGB functions 0.6,0.6,0.6
# First shadow, and so on
splot 2*r*u-1.5*r, d, v w pm3d,\
2*r*u-v/(d-e)*r-r, (d-e)*v+e, 0 w pm3d,\
2*r*u+1-1.5*r, d, 2*v w pm3d,\
2*r*u-v/(d-e)*r+1-r, (d-e)*v+e, 0 w pm3d,\
2*r*u+2-1.5*r, d, 1.5*v w pm3d,\
2*r*u-v/(d-e)*r+2-r, (d-e)*v+e, 0 w pm3d,\
2*r*u+3-1.5*r, d, 1.8*v w pm3d,\
2*r*u-v/(d-e)*r+3-r, (d-e)*v+e, 0 w pm3d,\
2*r*u+4-1.5*r, d, 1.1*v w pm3d,\
2*r*u-v/(d-e)*r+4-r, (d-e)*v+e, 0 w pm3d

set label 1 '1987' at 0, 0.6, 0 rotate by 30
set label 2 '1988' at 1, 0.6, 0 rotate by 30
set label 3 '1989' at 2, 0.6, 0 rotate by 30
set label 4 '1990' at 3, 0.6, 0 rotate by 30
set label 5 '1991' at 4, 0.6, 0 rotate by 30

set palette model RGB functions 0, 0, 1
f(u, xx) = r*cos(2*u*pi)+xx
g(u, yy) = r*sin(2*u*pi)+yy
splot f(u,0), g(u,e), 0 w l lt -1 lw a, f(u,0),g(u,e),v w pm3d, f(u,0), g(u,e),1 w l lt -1 lw b,\
f(u,1), g(u,e), 0 w l lt -1 lw a, f(u,1),g(u,e),2*v w pm3d, f(u,1), g(u,e), 2 w l lt -1 lw b,\
f(u,2), g(u,e), 0 w l lt -1 lw a, f(u,2),g(u,e),1.5*v w pm3d, f(u,2), g(u,e), 1.5 w l lt -1 lw b,\
f(u,3), g(u,e), 0 w l lt -1 lw a, f(u,3),g(u,e),1.8*v w pm3d, f(u,3), g(u,e), 1.8 w l lt -1 lw b,\
f(u,4), g(u,e), 0 w l lt -1 lw a, f(u,4),g(u,e),1.1*v w pm3d, f(u,4), g(u,e), 1.1 w l lt -1 lw b
unset multiplot

The first part of the code is just general setup, which determines how our figure will be scaled. The only thing to watch out for is the definitions of a, b... f. These are needed, because otherwise the aspect ratio of the cylinders would change, and they would be elongated along one (probably the y) axis. Therefore, it is essential to set the xrange and yrange to the same value.

In the figure, the actual graph has a background, which is yellow for the vertical planes, and gray for the horizontal one. We add these as separate plots in a multiplot command. So,

reset
...
set parametric
...
set urange [0:1]
set vrange [0:1]
...
# First, we draw the 'box' around the plotting volume
set palette model RGB functions 0.8, 0.8,0.8
splot 10*u-0.5, c+f*v,0 w pm3d

set palette model RGB functions 1, 254.0/255.0, 189.0/255.0
splot -0.5, c+f*u, 2.5*v w pm3d , 10*u-0.5, d, 2.5*v w pm3d

plots three planes, below, behind and next to the graph. I would point out that we used parametric plot, which we defined with 'set parametric' and the 'set urange', 'set vrange' commands. The second point of interest is the colouring of the planes: we do this by setting a palette, which contains only one colour, e.g., light gray,

set palette model RGB functions 0.8, 0.8,0.8

or

set palette model RGB functions 1, 254.0/255.0, 189.0/255.0

The next step is to plot the shadows of the bars. This is done by drawing rectangles of the proper size on the back plane, and also, by drawing parallelograms on the horizontal plane. These are drawn in a slightly darker shade of gray, so we have got to re-define our palette.

Once we are done with the shadows, we set the labels, which will just be the values of the first column in our data file. We have got to rotate the labels by 30 degrees, so that they will be parallel to the edge of our box.

Finally, we have got to plot the bars themselves. First, we choose a colour for them, blue in this case, and set the palette accordingly. If we simply plotted cylinders using 'pm3d', we wouldn't have edges, or we would have too many. In order to avoid this situation, we put on the two rims of the cylinder by hand. This is why each cylinder consists of actually three plots: the bottom, the surface and the top. Note that the cylinders are open, they only look closed because we can't see to the bottom of them. This means that you have got to be a bit careful when setting the 'view' (which we didn't do here, we simply took the default value of 60,30).
There you have the shaded 3D bars.

If you are using gnuplot, I assume that you also use Linux. If that's the case, this whole procedure can easily be scripted, so then you wouldn't have to set everything by hand. I might post a possible implementation sometime later.

Multiple layers on the same plot

This time, we will look at how to plot in three dimensions in an appealing way. For the sake of example, I will take the time evolution of the amplitude of water ripples after a point-like disturbance upsets the surface. Without going into details, I simply assume that the surface can be described by the zeroth Bessel function.

As a couple of times before, we will use multiplot to align the various figures. Here is the code

reset
set palette rgbformulae 33, 13, 10
set cbrange [-0.3:1]
a=-0.1
b=0.13
set multiplot
unset ztics
unset xtics
unset ytics
set size 1.1, 0.5
set samples 100,100
set isosamples 100, 100
set origin 0,a
set border 0
unset colorbox
unset key
set view 55,30
set xlabel 'x'
set ylabel 'y'
sp besj0(x*x+y*y) w pm3d at b
unset xlabel
unset ylabel
set origin 0,a+b
sp besj0(x*x/1.2+y*y/1.2)/1.2 w pm3d at b
set origin 0,a+2*b
sp besj0(x*x/1.4+y*y/1.4)/1.4 w pm3d at b
set origin 0,a+3*b
sp besj0(x*x/1.65+y*y/1.65)/1.65 w pm3d at b
set origin 0,a+4*b
sp besj0(x*x/1.95+y*y/1.95)/1.95 w pm3d at b
set origin 0,a+5*b
set arrow 1 from screen 0.1, 0.1 to screen 0.1, 0.8
set label 1 "time" at screen 0.08, 0.45 centre rotate by 90
sp besj0(x*x/2.2+y*y/2.2)/2.2 w pm3d at b
unset multiplot

And here is the figure that it produces

As you can see, as time goes on, the waves move radially outwards. (You shouldn't be carried away by the exact time evolution. This is only a demonstration:) Basically, we plot the functions on maps, and each time we translate the position of the new plot.

Gnuplot tricks

Many say that it is impossible to produce a publication quality plot with gnuplot. I strongly
believe that this assertion is simply wrong, and once you know what and how to do, gnuplot is
just as good as it gets. Of course, one shouldn't forget that gnuplot is a plotting utility, and
one won't have the conveniencies of FFT and the like, but this would be off the point.

In the following pages, I explain a couple of tricks that will help you produce high-quality
plots with gnuplot. While I understand the advantages of using a point-and-click type plotting
utility (e.g. Origin under Windows, Kst, Grace, Labplot under Linux), there are certain things
that are just much easier with gnuplot, once you get the hang of it.

Including unconventional symbols in a graph

So, you want to make a decent-looking, publication quality plot, with a couple of fancy
symbols here and there. There are several ways to go.

Enhanced EPS

If all you need is a couple of greek symbols and the like, then the easiest route is to use
the postscript terminal with the enhanced option, and simply enter the code for that particular
letter. (postscript is not the only terminal that has an enhanced option, however, the
degree to which those terminals are properly implemented is varying. Postscript works perfectly,
while others don't.) So, you would write

set terminal postscript eps enhanced solid "Helvetica" 14

and then, if you want to have a label with an α in it, you write

set label 1 at graph 0.1, 0.1 "{/Symbol a}^2 = 12"

which, once you set the output and replot your graph, will place
α²=12 at position (0.1,0.1) on your figure. You can find all available
characters and their corresponding code in Dick Crawford's
postscript guide

While setting the characters is quite easy, the problem with this method is that the character set is somewhat limited (though, almost always enough), and that the relative placement of the characters must be done manually, through trial and error. E.g., you would have a hard time, if you tried to write an overhead vector on some symbol. If this is the case, then you should use the epslatex terminal of gnuplot. We cover this subject in the next paragraph.

Using the epslatex terminal

As always, first we have to set our terminal as

set terminal epslatex

At this point, we can set labels with any LaTeX symbols, the generated output will contain it properly. For the sake of example, we will plot the error function, and write its definition on the figure as follows:

set terminal epslatex
set xrange [-3:3]
set yrange [-1:1]
set label 1 at -2, 0.5 "$erf(x) = \\frac{2}{\\sqrt{\\pi}}\\int_0^x\\, dt e^{-t^2}$" centre
plot erf(x)

Note that we have crammed a lot of LaTeX commands in the label, enclosed by the two $ signs, to indicate that we are dealing with mathematical expressions. You might have to escape the instructions twice, so you will have \\frac{}{} etc.

Now, if you set your output

set output 'errorf.tex'

and replot your graph, you will get two files. (At this point, I would also recommend re-setting the terminal, otherwise, there is no guarantee that gnuplot has closed both your output files, and this could create some trouble later on.) errorf.eps will contain the "visual" part of the graph, i.e., the axes, tics, points, lines, arrows and the like, while errorf.tex holds all the typographic elements. We then have got to combine these two by invoking LaTeX or pdflatex, depending on the exact route you would like to follow. The destination is the same in both cases.

So, let us suppose for the moment that you want to work with postscript, and not with pdf. You should create a LaTeX file, which includes nothing but the file that we have just produced, errorf.tex.

\documentclass{article}
\usepackage{graphics}
\usepackage{nopageno}
\usepackage{txfonts}
\usepackage[usenames]{color}

\begin{document}
\begin{center}
\input{errorf.tex}
\end{center}
\end{document}

You can read everything about epslatex in the gnuplot documentation. If you
want to compile with pdflatex, first you have to convert the postscript file to pdf. In principle, one could use the pdf terminal of gnuplot, but I have had problems with that, and the end result is far from the expected. I would recommend using the eps terminal, and then converting the file by

ps2pdf -dEPSCrop error.eps error.pdf

Of course, this assumes that you have ghostview installe on your computer. By passing the -dEPSCrop argument to ps2pdf, we can retain the bounding box in the eps file, so the pdf graph won't be bigger. By this time, you should have something like this figure:

Plotting on top of a map

Sometimes you might want to have overlapping plots. The first thing that comes to my mind
is a map, on which you would like to show a function that you have fitted to the peaks. An
example is shown in the figure below. It works only with gnuplot 4.3 or later, though.

We will have to use multiplot. The standard way is to tell gnuplot what, where and in what
size we want to plot, as in

set multiplot
set size 0.5, 1
set origin 0,0
plot sin(x)

set origin 0.5, 0
plot cos(x)
unset multiplot

The problem here is that when gnuplot determines how big the actual plot is going to be, it
counts the borders, axis label, tics and so on in the size. So, in the example above, the
width of 0.5 is the full with of one plot, and not the size of the plotting are, where the
curve is shown. Thus, when putting two plots on top of each other, strange things might happen.
The difficulty is that the second plot shouldn't contain axis labels, tics and so on. However,
when one takes those off, there is no telling as to what the final size of that graph is going
to be, and when they are on top of each other, there is a fair chance that they will be
misaligned.


In order to alleviate the situation, we have to force gnuplot to allocate a certain amount of
space for the curves, regardless the surroundings. We can do this with the command

set lmargin at screen 0.10
set rmargin at screen 0.85
set bmargin at screen 0.15
set tmargin at screen 0.95

where the four margins determine the white space on the left, right, bottom, and top,
respectively. This won't work on gnuplot 4.2 or earlier. Once we have specified the margins,
the rest is plain sailing. We plot both figures, and they will be aligned and top of each other.

The gnuplot commands that produced this figure are

reset
set terminal postscript enhanced eps solid colour "Helvetica" 22
unset key
set multiplot
set lmargin at screen 0.10
set rmargin at screen 0.85
set bmargin at screen 0.15
set tmargin at screen 0.95
set pm3d map
set palette rgbformulae 33,13,10
set xrange [0:1279]
set yrange [0:255]
set cbrange [4e4:2e5]
set cbtics ("4" 4e4, "8" 8e4, "12" 12e4, "16" 16e4, "20" 20e4)
set xlabel 'Pixel'
set ylabel 'Grey value'
splot 'shiftimage.dat' mat
unset xtics
unset ytics
unset xlabel
unset ylabel
p 'peak1.dat' using 2:0 with lines lt 3, 'peak2.dat' using 2:0 with lines lt 3
unset multiplot

(Obviously, you should replace the file names with some appropriate ones.)

Incidentally, the same method can be used to plot things that are not on top of each other,
but should still be aligned, as in the example below, where on the bottom, a horizontal, while
on the left hand side, a vertical cut through the centre are shown.

And here is the code producing this graph

reset
set out 'multi.svg'
set term svg size 600,400 dynamic enhanced fname 'arial' fsize 11 butt solid
set multiplot
set lmargin screen 0.20
set rmargin screen 0.85
set bmargin screen 0.25
set tmargin screen 0.90

set pm3d map
set palette rgbformulae 33,13,10
set samples 50, 50
set isosamples 50, 50
set xrange [ -15.00 : 15.00 ]
set yrange [ -15.00 : 15.00 ]
set cbrange [ -0.250 : 1.000 ]
set cbtics -0.25,0.25,1

unset xtics
unset ytics
unset key

splot sin(sqrt(x**2+y**2))/sqrt(x**2+y**2)
unset pm3d
set lmargin screen 0.10
set rmargin screen 0.20
set ytics

set parametric
set dummy u,v
set view map

f(h) = sin(sqrt(h**2))/sqrt(h**2)

set urange [ -15.00 : 15.00 ]
set vrange [ -15.00 : 15.00 ]
set xrange [*:*]
set surface

splot f(u), u, 0 with lines lc rgb "green"

unset parametric
set lmargin screen 0.20
set rmargin screen 0.85
set bmargin screen 0.10
set tmargin screen 0.25
set xrange [ -15.00 : 15.00 ]
set yrange [ * : * ]
set xtics
unset ytics

plot sin(sqrt(x**2))/sqrt(x**2)
unset multiplot

Broken axes in gnuplot

A broken axis definitely comes handy, if part of a curve doesn't contain too much relevant
information. Unfortunately, there is no easy way to do this in gnuplot. On the other hand, there is a work-around that can be applied in most situations. However, this method requires version 4.3
or later, so, if you don't have it, you should check it out on the development page.

For the sake of example, we will learn how to plot the cosine function in the [0:6π]
interval with a break point at 2.5π and 4.5π.

First, we have to determine what is the ratio of the two parts of the figure. Since the first
half is 2.5π long, while the second is 1.5π, we have to split the figure in a 2.5:1.5
ratio. I will choose 0.8 for the length of the whole figure (without the gap), so the first
half will be 0.5 long, while the second 0.3. We then insert the first half in a multiplot,
while keeping in mind that this part will have only three boundaries: left, bottom, and top.
The border is defined as the sum of bottom (1), left (2), top (4), and right (8).

set multiplot
unset key
unset xlabel
set border 1+2+4
set lmargin at screen 0.10
set rmargin at screen 0.6
set bmargin at screen 0.15
set tmargin at screen 0.95

Then, we specify the range and the tic marks

set ytics -1,0.5,1 nomirror
set xrange [0:2.5*pi]
set xtics ("0" 0, "{/Symbol p}" pi, "2{/Symbol p}" 2*pi)

and we also add the two slanted tics that denote the broken axis. These will just be two
arrows with no heads.

set arrow 1 from 2.5*pi-tiny, -1-tiny to 2.5*pi+tiny, -1+tiny nohead
set arrow 2 from 2.5*pi-tiny, 1-tiny to 2.5*pi+tiny, 1+tiny nohead

Now, that we are done with the outline of the first half, we plot the function, cosine in this
case.

plot cos(x)

The second half is very similar, with some small differences: First, this graph will still have
three boundaries, but on the bottom, right, and top. We also have to take off the vertical tics,
and keep an eye on the position of the graph. Therefore, we have

unset ytics
set border 1+4+8
set key right
set lmargin at screen 0.63
set rmargin at screen 0.93
set bmargin at screen 0.15
set tmargin at screen 0.95
set label 1 'cos(x)' at screen 0.5, 0.05 centre
set xrange [4.5*pi:6*pi]
set xtics ("5{/Symbol p}" 5*pi, "6{/Symbol p}" 6*pi)
set arrow 1 from 4.5*pi-tiny, -1-tiny to 4.5*pi+tiny, -1+tiny nohead
set arrow 2 from 4.5*pi-tiny, 1-tiny to 4q.5*pi+tiny, 1+tiny nohead
plot cos(x)
unset multiplot

At the end of the plot, we closed the multiplot, and also added an xlabel, which is located
at the centre of the whole graph. After setting the appropriate terminal, we get a figure
that looks like this:

It's quite re-assuring that the cosine function has the same value at 2.5π and 4.5π.
You would have never guessed, would you?

Plotting a histogram

From version 4.3, there is an option to plot data in a histogram, but this hasn't always been
the case. However, there is a way to rectify the situation, using the smooth option.
First, we have to define our bins, and then we have got to count the number of data points
falling into each of the bins. The frequency specifier of the smooth option takes care
of this, and we only have to determine into which bin a particular data point falls. The
bin(x, width) function will do this; its working should be obvious. As an example, we take
10000 numbers normally distributed between 0 and 6, and plot their frequency. At the same
time, we can also plot the cumulative frequency, which is another specifier of the smooth
option.

unset key
set ylabel 'Frequency'
set y2label 'Cumulative frequency'
set y2tics 0,2e3,1e4
set ytics nomirror
set boxwidth 0.7 relative
set style fill solid 0.5
f(x) = a*exp(-(x-b)*(x-b)/c/c)
a=560.0
b=3.0
c = 1.0
bw = 0.1
bin(x,width)=width*floor(x/width)
plot 'gauss.dat' using (bin($1,bw)):(1.0) smooth frequency with boxes,\
'' using (bin($1,bw)):(1.0) smooth cumulative axis x1y2 w l lt 2 lw 2, \
f(x) w l lt 3 lw 2

Coloured axes

Sometimes you might need a left and a right vertical axis with different colours, to signify
the scale that belongs to two curves shown on the graph. We will discuss an easy way to achieve
this effect. Since we cannot set the colour of the axes one by one, we will do this in two
steps. Let us suppose that the two axes should be red and blue.


First, we draw the border that is meant to be red. The command

set border 1+2 lt 1

sets the left and the bottom axis red, which is linetype 1. The top and the right axes are not
drawn at this moment. We will plot sin(x) on the left axis.
Then we draw two blue arrows without heads where the right and the top axes are
supposed to be, as in

set arrow 1 from 10, -1 to 10, 1 nohead lt 3
set arrow 2 from -10,  1 to 10, 1 nohead lt 3

The function on the right axis will be exp(x)|sin(x)|, although it doesn't really matter. The
rest of the code sets up the tics, label colours and the like. There is only one small thing
worth looking at: when we specify the format of y2tics, we give it as format "10^{%T}", where
%T is a format specifier, and it tells gnuplot to substitute the exponent of the 10-base
value of the y2tics. Using specifiers like this, very nice results can be obtained. I will cover
this subject in a later post.

reset
unset key
set border 1+2 lt 1
set y2tics 1e-5, 1e2, 1e5 textcolor rgb "blue" format "10^{%T}"
set ytics nomirror format "%.1f"
set xtics nomirror
set xlabel 'x' textcolor rgb "red"
set ylabel 'sin(x)' textcolor rgb "red"
set y2label 'exp(x)|sin(x)|' textcolor rgb "blue"
set log y2
set arrow 1 from 10, -1 to 10, 1 nohead lt 3
set arrow 2 from -10,  1 to 10, 1 nohead lt 3
set sample 1000
plot sin(x) with lines lt 1, exp(x)*abs(sin(x)) with lines lt 3 axis x1y2

After plotting the two functions, we would get a graph like this:

If the colour of the tics on y2 still bothers you, you can change it by tampering with the
eps file.