Broken histograms

Sometimes, a histogram is just a bit awkward, for the simple reason that one or two values are extremely high compared to the rest of the graph. In the case of a standard graph, we would use a broken axis to bring all points to the same order of magnitude. We can play the same trick with histograms, in fact, it is, in some sense, even simpler, than the broken axes. All we have to do is to plot a thick line at the proper position in the proper colour. This is the graph that we are going to make today

Our data file, brokenhist.dat, is as follows

"Jan" 1 2
"Feb" 44 4
"Mar" 3 1
"Apr" 2 25
"May" 4 5
"June" 2 1

and here is our script:

reset
blue = "#babaff"
set xrange [-0.5:5.5]
set yrange [0:11]
set isosample 2, 100
set table 'brokenhist_b.dat'
splot 1-exp(-y/2.0)
unset table

unset colorbox
set border 1
set xtics rotate by 45 nomirror offset 0, -1
unset ytics
f(x) = (x < 6 ? x : (x < 30 ? x-17 : x-35) )
g(x) = (x < 6 ? 1/0 : 6)
set boxwidth 0.85
set style fill solid 0.8 border -1
set style data histograms
set palette defined (0 "#ffff   ff", 1 "#babaff")
plot 'brokenhist_b.dat' w ima,\
'brokenhist.dat' u (f($2)) t 'Red bars',\
'' u (f($3)) lc rgb "#00bb00" t 'Green bars', \
'' u 0:(f($2)):2 w labels center offset 0,0.5 t '',\
'' u ($0+0.25):(f($3)):3 w labels center offset 0,0.5 t '',\
'' u 0:(-1):xticlabel(1) w l t '', \
'' u ($0+0.12):(g($3)+0.12):(0.25):(0.25) w vectors lt -1 lc rgb blue lw 5 nohead t '', \
'' u ($0-0.12):(g($2)+0.12):(0.25):(0.25) w vectors lt -1 lc rgb blue lw 5 nohead t ''

OK, so let us look at the code! The first couple of lines are required only, if you want to have some posh background. Likewise, you can drop the 'unset colorbox' line, when you have a white background. We set only the bottom axis, which means that we have to unset the ytics and set to xtics to nomirror. Then we have two helper functions. The definitions of these depend on where you want to have the break point in the histogram. In this particular case, I took 6, but it is arbitrary.

In the next step, we set the properties of the histogram, like the width of the columns, the fill style, and the data style. We also define a palette, but this is needed for the background only. For white background, you can skip this step. You can also skip the first plot, because that is nothing but our fancy background.

The actual plotting begins after this. We plot the two sets of columns, and also plot the data file with labels. The labels are placed at the top of each column (this is why we could do away with the yaxis.) We also 'plot' the axis labels, and finally, plot the two break points. Note that the plotting of the break points is automatic, once we have the definitions of the two helper functions. If you want to have a steeper cut, you could

'' u ($0+0.12):(g($3)+0.12):(0.25):(0.5) w vectors lt -1 lc rgb blue lw 5 nohead t ''

e.g., which stretches the vectors in the vertical direction. Otherwise, we have finished the plot, there is nothing else to do.
I should point out here that, in order to have a seamless cut, we have to use a colour for the vectors that is identical to the background at that particular point. This implies that we could not have a gradient at y=6. The background colour is virtually constant at y=6 (c.f. the definition of 'brokenhist_b.dat'. While it would not be impossible to implement a cut over a gradient, I believe, it is probably not worth the trouble it involves.

Update

I have had some time, so I moved all recent posts to their permanent place on
my web page. I have "sexed up" the homepage a bit, so, hopefully, browsing will be a tad easier. Let me know, if there are any problems! (I know that there is a small glitch with the cascaded style sheets on IE6. IE8 should work without problems. Firefox 3.5 is also OK.) There is a zipped version of the complete site, if you want to read it off-line.
Comments should still be posted here, please!

Cheers,
Zoltán

Some basic statistics with gnuplot

In my previous post, I mentioned a patch that you can compile into gnuplot, and that should make plots with some statistical properties a bit easier. Now, the problem with that patch is that, if you don't want to, or can't take the trouble of compiling gnuplot for yourself, it is no use. However, for most things contained in the patch, there is a work-around that should function properly in gnuplot 4.2. I will discuss those now.

The first thing I did with the statistical patch was to plot the mean, minimum and maximum of a data set. This can easily be done in the following way.

reset
# Produce some dummy data
set sample 200
set table 'stats2.dat'
plot [0:10] 0.5+rand(0)
unset table

set yrange [0:2]
unset key

# Retrieve statistical properties
plot 'stats2.dat' u 1:2
min_y = GPVAL_DATA_Y_MIN
max_y = GPVAL_DATA_Y_MAX

f(x) = mean_y
fit f(x) 'stats2.dat' u 1:2 via mean_y

# Plotting the minimum and maximum ranges with a shaded background
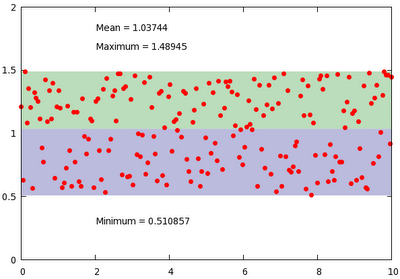
set label 1 gprintf("Minimum = %g", min_y) at 2, min_y-0.2
set label 2 gprintf("Maximum = %g", max_y) at 2, max_y+0.2
set label 3 gprintf("Mean = %g", mean_y) at 2, max_y+0.35
plot min_y with filledcurves y1=mean_y lt 1 lc rgb "#bbbbdd", \
max_y with filledcurves y1=mean_y lt 1 lc rgb "#bbddbb", \
'stats2.dat' u 1:2 w p pt 7 lt 1 ps 1

At the beginning of our script, we just produce some dummy data, and call a dummy plot. This plot does nothing but fills in the values of the minimum and maximum of the data set. Then we fit a constant function. You can convince yourself that this returns the average of the data set.

In the plotting section, we produce three labels that tell us something about the data set, and plot the data range with shaded region. Easy enough, and in just a couple of lines, we created this figure

Now, what should we do, if we were to calculate the standard deviation. Well, we know how to calculate the average, so we will use that. Here is the script:

reset
set sample 200
set table 'stats2.dat'
plot [0:10] 0.5+rand(0)
unset table

set yrange [0:2]
unset key
f(x) = mean_y
fit f(x) 'stats2.dat' u 1:2 via mean_y

stddev_y = sqrt(FIT_WSSR / (FIT_NDF + 1 ))

# Plotting the range of standard deviation with a shaded background
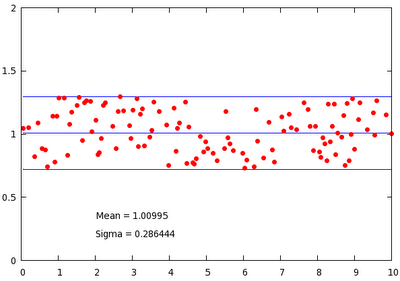
set label 1 gprintf("Mean = %g", mean_y) at 2, min_y-0.2
set label 2 gprintf("Standard deviation = %g", stddev_y) at 2, min_y-0.35
plot mean_y-stddev_y with filledcurves y1=mean_y lt 1 lc rgb "#bbbbdd", \
mean_y+stddev_y with filledcurves y1=mean_y lt 1 lc rgb "#bbbbdd", \
mean_y w l lt 3, 'stats2.dat' u 1:2 w p pt 7 lt 1 ps 1

What we utilise here is the fact that the fit function also sets a couple of variables. One of them is the sum of the residuals, which is called FIT_WSSR, while another is the number of degrees of freedom, FIT_NDF. However, we know that the number of degrees of freedoms is one less, than the number of data points, for we fit a function with a single parameter. Therefore, if we take the square root of the sum of residuals divided by the number of degrees of freedom plus one, we get the standard deviation. The rest of the plot is trivial, and this script results in the following graph:

Incidentally, this can also be used for removing points that are very far from the mean. The following script takes out those data that are more than one standard deviation away from the mean.

reset
set sample 200
set table 'stats2.dat'
plot [0:10] 0.5+rand(0)
unset table

set yrange [0:2]
unset key
f(x) = mean_y
fit f(x) 'stats2.dat' u 1:2 via mean_y

stddev_y = sqrt(FIT_WSSR / (FIT_NDF + 1 ))

# Removing points based on the standard deviation
set label 1 gprintf("Mean = %g", mean_y) at 2, min_y-0.15
set label 2 gprintf("Sigma = %g", stddev_y) at 2, min_y-0.3
plot mean_y w l lt 3, mean_y+stddev_y w l lt 3, mean_y-stddev_y w l lt 3, \
'stats2.dat' u 1:(abs($2-mean_y) < stddev_y ? $2 : 1/0) w p pt 7 lt 1 ps 1

with the corresponding figure

Only the last line is relevant: we use the ternary operator to decide whether we want to keep the point: if the deviation from the mean is less, than the standard deviation, we hold on to our data, otherwise, we replace it by 1/0, which is undefined, and gnuplot quietly ignores it. If you want to learn more about the working of the ternary operator, check out my post on the plotting of an inequality.

We have, thus, already found a solution for two of the problems addressed in the patch. What about the third one, adding arrows to the plot at the position of the minimum or maximum, say. We can do that, too. Here is the script:

reset
set sample 50
set table 'stats1.dat'
plot [0:10] 0.5+rand(0)
unset table

set yrange [0:2]
unset key
plot 'stats1.dat' u 1:2
min_y = GPVAL_DATA_Y_MIN
max_y = GPVAL_DATA_Y_MAX

plot 'stats1.dat' u ($2 == min_y ? $2 : 1/0):1
min_pos_x = GPVAL_DATA_Y_MIN
plot 'stats1.dat' u ($2 == max_y ? $2 : 1/0):1
max_pos_x = GPVAL_DATA_Y_MAX

# Automatically adding an arrow at a position that depends on the min/max
set arrow 1 from min_pos_x, min_y-0.2 to min_pos_x, min_y-0.02 lw 0.5
set arrow 2 from max_pos_x, max_y+0.2 to max_pos_x, max_y+0.02 lw 0.5
set label 1 'Minimum' at min_pos_x, min_y-0.3 centre
set label 2 'Maximum' at max_pos_x, max_y+0.3 centre
plot 'stats1.dat' u 1:2 w p pt 6

First, we retrieve the values of the minimum and the maximum by using a dummy plot. Having done that, we retrieve the positions of the minimum and maximum, by calling a dummy plot on the columns

plot 'stats1.dat' u ($2 == min_y ? $2 : 1/0):1

What this line does is substitute min_y, when the second column (whose minimum we extracted before) is equal to the minimum, and an undefined value, 1/0, otherwise. The minimum of this plot is nothing, but the x position of the first minimum. Likewise, had we assigned

min_pos_x = GPVAL_DATA_Y_MAX

that would have given the position of the last minimum of the data file. Obviously, these distinctions make sense only, if there are more than one minimum or maximum. Knowing the x and y positions of the minimum and maximum, we can easily set the arrows. We, thus, have the following figure

Adding labels showing the value should not be a problem now.

Well, this is for today. Till next time!

Patching gnuplot

One of the major advantages of open-source code is that if you would like to add some new features, you can easily do that. This applies to gnuplot, too, in fact, doing that does not require anything special. I have been quite inactive on this blog recently, and the reason is that Philipp Janert and I have been working on a patch to gnuplot.

The steps of patching gnuplot are described on gnuplot's main web page. There are a number of patches uploaded to gnuplot's patch tracker, on which quite a few new features, still in the development phase, are published. It is really worthwhile to try them out, first, to provide feedback as to what is useful and what is not, and second, to help the developers to find bugs and other glitches, like what the syntax of a command should be and so on.

Our patch is related to an old debate as to what gnuplot really is. At many a place, you will find the statement that "gnuplot is a plotting utility, not a statistical analysis package". I have nothing against this statement, however, when saying so, we have to tell what we mean by plotting. So, is plotting just placing a thousand dots at positions that represent our data? Or do we want more? E.g., throwing out data points that are unreasonably far from the mean. Or showing the mean, and the standard deviation? Or calling the reader's attentional to some special points, like the minimum or the maximum in a data set? And many similar things. I believe, plotting requires much more, than just showing the measurement data: a plot makes sense only, if we can point out what is to be pointed out. By the way, fitting falls into this category, and fitting has been an integral part of gnuplot for ages. The point being that the original statement (gnuplot is a plotting utility, not a statistical analysis package) has been wrong for a long time.

The patch that I mentioned above was announced yesterday on the gnuplot development mailing list and you can find the patch for the source and the
documentation on patch tracker. I have put a couple of examples on my gnuplot web site under patch. You can also find the full documentation.

I would like to ask you, if you feel crafty and you can, download the patch, and try it, and let us know whether you find it useful, what else, do you think, we could do with it and so on. It would really help the development. Once the patch makes it to the main code, I will discuss various option on these pages.

Just to wet your appetite, here is a figure that you could very easily make with the new patch. (You can find the code on my web site.)

Many cheers,
Zoltán